在神经网络中使用激活函数

S 型函数和消失梯度

sigmoid 激活函数是神经网络非线性激活函数的流行选择。它受欢迎的原因之一是它的输出值在 0 到 1 之间，模拟概率值。因此，它用于将线性层的实值输出转换为概率，该概率可以用作概率输出。这也使得它成为逻辑回归方法的重要组成部分，可以直接用于二元分类。

sigmoid 函数通常用 $\sigma$ 表示，其形式为 $\sigma = \frac{1}{1 + e^{-1}}$。在 TensorFlow 中，您可以从 Keras 库调用 sigmoid 函数，如下所示：�并具有以下形式�=11+�-1。在 TensorFlow 中，您可以从 Keras 库调用 sigmoid 函数，如下所示：

这给出了以下输出：

您还可以将 sigmoid 函数绘制为 $x$ 的函数，�,

S 型激活函数

在查看神经网络中神经元的激活函数时，您还应该对其由于反向传播和链式法则而产生的导数感兴趣，这会影响神经网络从数据中学习的方式。

Sigmoid 激活函数（蓝色）和梯度（橙色）

在这里，您可以观察到 sigmoid 函数的梯度始终在 0 到 0.25 之间。当 $x$ 趋于正无穷大或负无穷大时，梯度趋于零。这可能会导致梯度消失问题，这意味着当输入处于 $x$ 的某个较大幅度时（例如，由于较早层的输出），梯度太小而无法启动校正。�趋于正无穷或负无穷，梯度趋于零。这可能会导致梯度消失问题，这意味着当输入处于某个较大的幅度时�（例如，由于较早层的输出），梯度太小而无法启动校正。

梯度消失是一个问题，因为链式法则用于深度神经网络的反向传播。回想一下，在神经网络中，每一层（损失函数）的梯度是其后续层的梯度乘以其激活函数的梯度。由于网络中有很多层，如果激活函数的梯度小于1，则远离输出的某些层的梯度将接近于零。任何梯度接近于零的层都会停止梯度传播进一步返回到较早的层。

由于 sigmoid 函数始终小于 1，因此具有更多层的网络会加剧梯度消失问题。此外，存在一个sigmoid梯度趋于0的饱和区域，即$x$的幅度较大的区域。因此，如果前一层激活的加权和的输出很大，那么通过该神经元传播的梯度将非常小，因为激活 $a$ 相对于激活函数的输入的导数会很小（在饱和区）。�很大。因此，如果前一层激活的加权和的输出很大，那么您将有一个非常小的梯度通过该神经元传播作为激活的导数�相对于激活函数的输入会很小（在饱和区域）。

当然，还存在线性项相对于前一层激活的导数，该导数对于该层可能大于 1，因为权重可能很大，并且它是来自不同神经元的导数之和。然而，在训练开始时它仍然可能引起关注，因为权重通常初始化得很小。

双曲正切函数

另一个需要考虑的激活函数是 tanh 激活函数，也称为双曲正切函数。与sigmoid函数相比，它具有更大的输出值范围和更大的最大梯度。tanh 函数是大多数人所熟悉的圆的法线正切函数的双曲类比。

绘制 tanh 函数：

Tanh 激活函数

我们也看看梯度：

Tanh 激活函数（蓝色）和梯度（橙色）

请注意，与 sigmoid 函数相比，梯度现在的最大值为 1，其中最大梯度值为 0。这使得具有 tanh 激活的网络不易受到梯度消失问题的影响。然而，tanh 函数也有一个饱和区域，其中梯度值随着输入 $x$ 的大小变大而趋于趋于饱和。�变大。

tanh在 TensorFlow 中，您可以使用Keras 激活模块中的函数在张量上实现 tanh 激活：

这给出了输出：

1	tf.Tensor([–0.7615942  0.         0.7615942], shape=(3,), dtype=float32)

修正线性单元 (ReLU)

最后要详细介绍的激活函数是整流线性单元，也通常称为 ReLU。由于其计算相对简单，它最近变得流行。这有助于加速神经网络，并且似乎获得了经验上良好的性能，这使其成为激活函数的良好起始选择。

ReLU 函数是一个简单的 $\max(0, x)$ 函数，也可以将其视为分段函数，所有小于 0 的输入映射到 0，所有大于或等于 0 的输入映射回自身（即恒等函数）。从图形上看，最大限度（0,�）函数，它也可以被认为是一个分段函数，所有小于 0 的输入映射到 0，所有大于或等于 0 的输入映射回自身（即恒等函数）。从图形上看，

ReLU激活函数

接下来，您还可以查看 ReLU 函数的梯度：

ReLU激活函数（蓝线）和梯度（橙色）

请注意，只要输入为正，ReLU 的梯度就是 1，这有助于解决梯度消失问题。然而，只要输入为负，梯度就是 0。这可能会导致另一个问题，即死亡神经元/垂死 ReLU 问题，如果神经元持续失活，这就是一个问题。

在这种情况下，神经元永远无法学习，并且由于链式法则，其权重永远不会更新，因为它的其中一项梯度为 0。如果数据集中的所有数据都发生这种情况，那么该神经元就很难从数据集中学习，除非前一层中的激活发生变化，使得神经元不再“死亡”。

要在 TensorFlow 中使用 ReLU 激活：

1 2 3 4 5

import tensorflow as tf from tensorflow.keras.activations import relu input_array = tf.constant([–1, 0, 1], dtype=tf.float32) print (relu(input_array))

这给出了以下输出：

1	tf.Tensor([0. 0. 1.], shape=(3,), dtype=float32)

上面回顾的三个激活函数表明它们都是单调递增函数。这是必需的；否则，您无法应用梯度下降算法。

现在您已经探索了一些常见的激活函数以及如何在 TensorFlow 中使用它们。让我们看看如何在实际模型中使用它们。

在实践中使用激活函数

在探索激活函数在实践中的使用之前，让我们看一下将激活函数与另一个 Keras 层组合时使用激活函数的另一种常见方法。假设您想在 Dense 层之上添加 ReLU 激活。按照上述方法执行此操作的一种方法是：

1 2	x = Dense(units=10)(input_layer) x = relu(x)

但是，对于许多 Keras 层，您还可以使用更紧凑的表示在层顶部添加激活：

1	x = Dense(units=10, activation=”relu”)(input_layer)

使用这种更紧凑的表示，让我们使用 Keras 构建 LeNet5 模型：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

import tensorflow as tf import tensorflow.keras as keras from tensorflow.keras.layers import Dense, Input, Flatten, Conv2D, BatchNormalization, MaxPool2D from tensorflow.keras.models import Model (trainX, trainY), (testX, testY) = keras.datasets.cifar10.load_data() input_layer = Input(shape=(32,32,3,)) x = Conv2D(filters=6, kernel_size=(5,5), padding=“same”, activation=“relu”)(input_layer) x = MaxPool2D(pool_size=(2,2))(x) x = Conv2D(filters=16, kernel_size=(5,5), padding=“same”, activation=“relu”)(x) x = MaxPool2D(pool_size=(2, 2))(x) x = Conv2D(filters=120, kernel_size=(5,5), padding=“same”, activation=“relu”)(x) x = Flatten()(x) x = Dense(units=84, activation=“relu”)(x) x = Dense(units=10, activation=“softmax”)(x) model = Model(inputs=input_layer, outputs=x) print(model.summary()) model.compile(optimizer=“adam”, loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics=“acc”) history = model.fit(x=trainX, y=trainY, batch_size=256, epochs=10, validation_data=(testX, testY))

运行此代码会产生以下输出：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50

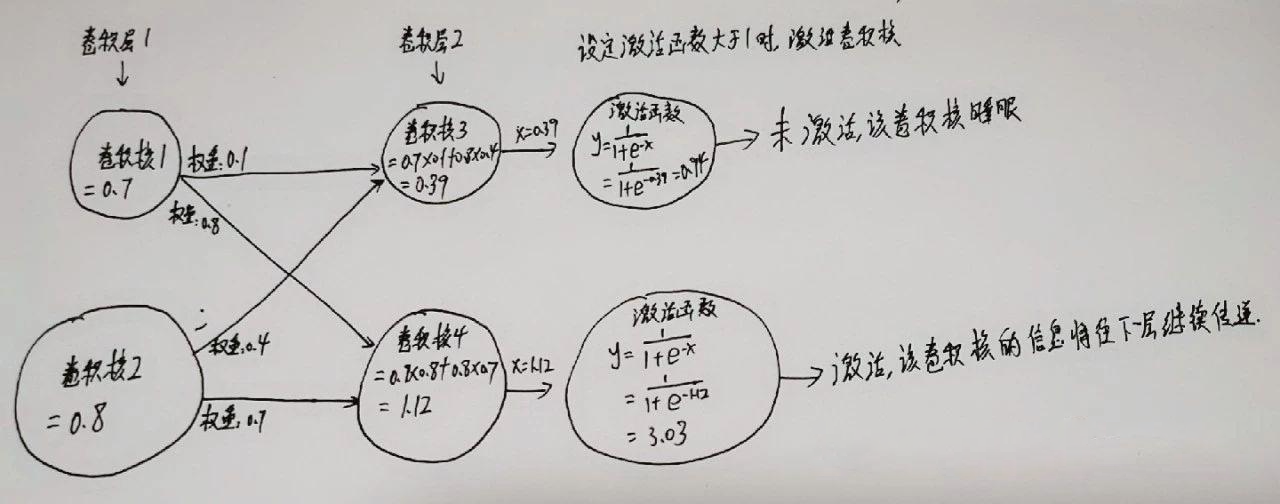
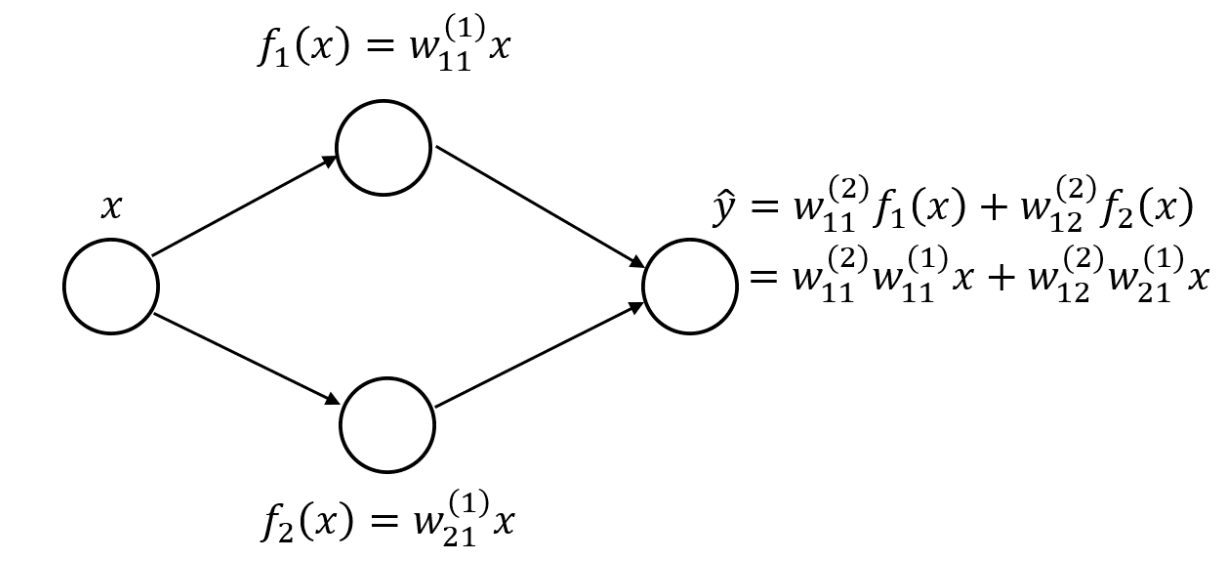
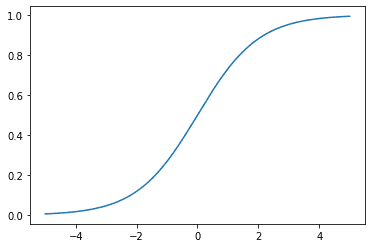
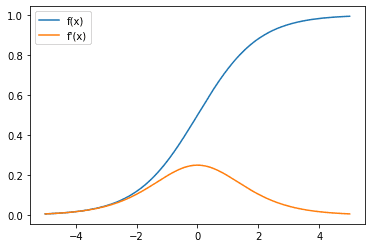
Model: “model” _________________________________________________________________ Layer (type)                Output Shape              Param # ================================================================= input_1 (InputLayer)        [(None, 32, 32, 3)]       0 v2d (Conv2D)             (None, 32, 32, 6)         456 max_pooling2d (MaxPooling2D  (None, 16, 16, 6)        0 ) conv2d_1 (Conv2D)           (None, 16, 16, 16)        2416 max_pooling2d_1 (MaxPooling  (None, 8, 8, 16)         0 2D) conv2d_2 (Conv2D)           (None, 8, 8, 120)         48120 flatten (Flatten)           (None, 7680)              0 dense (Dense)               (None, 84)                645204 dense_1 (Dense)             (None, 10)                850 ================================================================= Total params: 697,046 Trainable params: 697,046 Non-trainable params: 0 _________________________________________________________________ None Epoch 1/10 196/196 [==============================] – 14s 11ms/step – loss: 2.9758 acc: 0.3390 – val_loss: 1.5530 – val_acc: 0.4513 Epoch 2/10 196/196 [==============================] – 2s 8ms/step – loss: 1.4319 – acc: 0.4927 – val_loss: 1.3814 – val_acc: 0.5106 Epoch 3/10 196/196 [==============================] – 2s 8ms/step – loss: 1.2505 – acc: 0.5583 – val_loss: 1.3595 – val_acc: 0.5170 Epoch 4/10 196/196 [==============================] – 2s 8ms/step – loss: 1.1127 – acc: 0.6094 – val_loss: 1.2892 – val_acc: 0.5534 Epoch 5/10 196/196 [==============================] – 2s 8ms/step – loss: 0.9763 – acc: 0.6594 – val_loss: 1.3228 – val_acc: 0.5513 Epoch 6/10 196/196 [==============================] – 2s 8ms/step – loss: 0.8510 – acc: 0.7017 – val_loss: 1.3953 – val_acc: 0.5494 Epoch 7/10 196/196 [==============================] – 2s 8ms/step – loss: 0.7361 – acc: 0.7426 – val_loss: 1.4123 – val_acc: 0.5488 Epoch 8/10 196/196 [==============================] – 2s 8ms/step – loss: 0.6060 – acc: 0.7894 – val_loss: 1.5356 – val_acc: 0.5435 Epoch 9/10 196/196 [==============================] – 2s 8ms/step – loss: 0.5020 – acc: 0.8265 – val_loss: 1.7801 – val_acc: 0.5333 Epoch 10/10 196/196 [==============================] – 2s 8ms/step – loss: 0.4013 – acc: 0.8605 – val_loss: 1.8308 – val_acc: 0.5417

这就是您在 TensorFlow 模型中使用不同激活函数的方式！