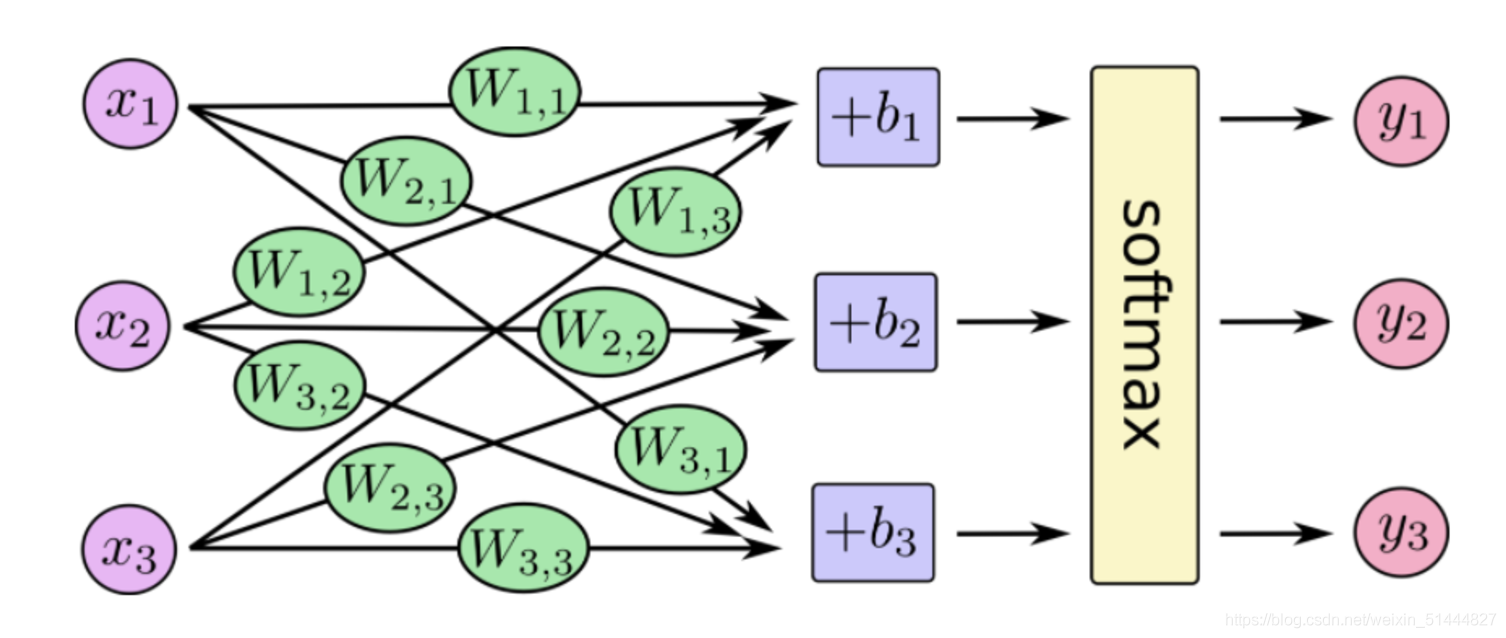
神经网络中批次和纪元的区别

随机梯度下降

随机梯度下降，简称 SGD，是一种用于训练机器学习算法的优化算法，尤其是深度学习中使用的人工神经网络。

该算法的工作是找到一组内部模型参数，这些参数对于某些性能指标（例如对数损失或均方误差）表现良好。

优化是一种搜索过程，您可以将这种搜索视为学习。该优化算法称为“梯度下降”，其中“梯度”是指误差梯度或误差斜率的计算，“下降”是指沿着该斜率向下移动到某个最小误差水平。

该算法是迭代的。这意味着搜索过程发生在多个离散步骤中，每个步骤都希望稍微改进模型参数。

每个步骤都涉及使用具有当前内部参数集的模型对某些样本进行预测，将预测与真实的预期结果进行比较，计算误差，并使用误差来更新内部模型参数。

对于不同的算法，该更新过程是不同的，但在人工神经网络的情况下，使用反向传播更新算法。

在我们深入研究批次和时期之前，让我们先看一下样本的含义。

在这里了解有关梯度下降的更多信息：

什么是样本？

样本是单行数据。

它包含输入到算法中的输入和用于与预测进行比较并计算误差的输出。

训练数据集由许多行数据组成，例如许多样本。样本也可以称为实例、观察、输入向量或特征向量。

现在我们知道什么是样本，让我们定义一个批次。

什么是批次？

批量大小是一个超参数，定义在更新内部模型参数之前要处理的样本数量。

将批次视为迭代一个或多个样本并进行预测的 for 循环。在批次结束时，将预测与预期输出变量进行比较并计算误差。根据该误差，使用更新算法来改进模型，例如沿着误差梯度向下移动。

训练数据集可以分为一批或多批。

当所有训练样本都用于创建一批时，该学习算法称为批量梯度下降。当批次大小为一个样本时，学习算法称为随机梯度下降。当批量大小大于一个样本且小于训练数据集的大小时，该学习算法称为小批量梯度下降。

• 批量梯度下降。批量大小 = 训练集大小
• 随机梯度下降。批量大小 = 1
• 小批量梯度下降。1 < 批量大小 < 训练集大小

在小批量梯度下降的情况下，流行的批量大小包括 32、64 和 128 个样本。您可能会在文献和教程的模型中看到这些值。

如果数据集没有除以批量大小怎么办？

在训练模型时，这种情况可能而且确实经常发生。这仅仅意味着最终批次的样本数量少于其他批次。

或者，您可以从数据集中删除一些样本或更改批次大小，以便数据集中的样本数量除以批次大小。

什么是纪元？

epoch 的数量是一个超参数，它定义了学习算法在整个训练数据集中工作的次数。

一个epoch意味着训练数据集中的每个样本都有机会更新内部模型参数。一个纪元由一个或多个批次组成。例如，如上所述，一个 epoch 具有一个批次，称为批次梯度下降学习算法。

您可以想象一个针对 epoch 数的 for 循环，其中每个循环都在训练数据集上进行。在这个 for 循环中是另一个嵌套的 for 循环，它迭代每批样本，其中一个批次具有指定的“批量大小”数量的样本。

历元的数量传统上很大，通常是数百或数千，允许学习算法运行直到模型的误差被充分最小化。您可能会在文献和教程中看到将 epoch 数量设置为 10、100、500、1000 或更大的示例。

通常创建线图，将 x 轴上的历元显示为时间，并在 y 轴上显示模型的误差或技能。这些图有时称为学习曲线。这些图可以帮助诊断模型是否学习过度、学习不足或是否适合训练数据集。

批次和纪元有什么区别？

批量大小是模型更新之前处理的样本数量。

纪元数是完整通过训练数据集的次数。

批次的大小必须大于或等于 1 且小于或等于训练数据集中的样本数。

纪元数可以设置为 1 到无穷大之间的整数值。您可以根据需要运行算法，甚至可以使用除固定周期数之外的其他标准来停止算法，例如模型误差随时间的变化（或缺乏变化）。

它们都是整数值，并且都是学习算法的超参数，例如学习过程的参数，而不是学习过程找到的内部模型参数。

您必须指定学习算法的批量大小和时期数。

对于如何配置这些参数并没有什么神奇的规则。您必须尝试不同的值，看看什么最适合您的问题。

工作示例

最后，让我们用一个小例子来具体说明这一点。

假设您有一个包含 200 个样本（数据行）的数据集，并且您选择的批量大小为 5 和 1,000 epoch。

这意味着数据集将分为 40 个批次，每个批次有 5 个样本。每批五个样本后将更新模型权重。

这也意味着一个 epoch 将涉及 40 个批次或模型的 40 次更新。

在 1,000 个 epoch 中，模型将暴露或通过整个数据集 1,000 次。整个训练过程总共有 40,000 个批次。